 The problem's target is try to find how many solutions exist, for
a \(N*N\) chess board.
The problem's target is try to find how many solutions exist, for
a \(N*N\) chess board.
In the class, we discussed the theory of linear arithmetic (shortened as LA in the following) and linear programming (shortened as LP in the following). Arithmetical constraints are ubiquitous in every aspect of formal reasoning and (hard) problem-solving, and both LA and LP are very powerful tools to establish these models and to solve the problems.
From the computer science point of view, most LA and LP problems can be solved by special-purpose software or libraries (e.g., the IBM's very popular CPLEX). However, most modern general-purpose solvers/provers also have good enough support for both LA and LP, by incorporating well-tuned decision procedures for LA/LP over the integers, rationals, or real domains. Take Z3 as an example, it has decent support for both LA and LP.
In this lab, you will be familiarizing yourself with the background theories of LA/LP, with the important applications of LA/LP to real-world (hard) problem (by using Z3), and with the underpinning algorithms of modern provers/solvers to solve these problems.
This lab is divided into three parts, each of which contains both some tutorials and problems. The first part introduces the basic background and knowledge of LA/LP theory; the second part discusses the applications of LA/LP theory, by solving some (NP-Complete hard) problems; and the third part covers the algorithm implementation including the Fourier-Motzkin variable elimination, and Simplex. Some problems are tagged with Exercise, which you should solve. And several problems are tagged with Challenge, which are optional. Download this code template to start with.
When you finished the lab, zip you code files with file name <ID>-lab-5.zip (e.g., SA19225789-lab-5.zip), and submit it to USTC Online Teaching Platform.
In this section, we will discuss the basic LA/LP theories, by using the solver Z3.
Recall from the lecture, the syntax for LA is:
A ::= x | c | c*x
E ::= A + E | A
R ::= E = E | E <= E | E < E
P ::= R | P /\ P
The solver Z3 has complete support for this syntax, and can solve these equalities/inequalities efficiently. For example, suppose we can have two numbers \(x, y\in \) ℝ, and the following constraints: \begin{cases} x + y = 0.8 \\ x - y = 0.2 \end{cases}
Then we can declare two Z3 variables and build the solver in Z3 as:
x, y = Reals('x y')
solver = Solver()
solver.add([x + y == 0.8, x - y == 0.2])
res = solver.check()
if res == sat:
print(solver.model())
else:
print("no solution")
and Z3 will output the model it finds, if the above constraints are satisfiable.
Of course, not all constraints are satisfiable, for example, consider the following constraints on two variables \(x, y \in \) ℤ: \begin{cases} x + y = 0.8 \\ x + y = 0.2 \end{cases} where $$ x,y \in ℤ, $$ obviously, these constraints are unsatisfiable.
Besides the domain real ℝ ("Reals"), Z3 also has decent support for the integer domain ℤ. For instance, for two integer variables \(x, y \in \) ℤ, this code
x, y = Ints('x y')
declares two integers \(x\) and \(y\) in Z3. Similarly, we can ask Z3 to check such constraints on Integers, for instance, given the following constraints: $$ \begin{cases} x + y = 8 \\ x - y = 2 \end{cases} $$ where $$ x,y \in \mathbb{Z}, $$ and give the model.
One key point to note here is that: when we talk about the satisfiability of constraints, we must make it clear what domains (ℝ, ℤ, ℚ or others?) we are working on, because the satisfiability of constraints is dependent on the underlying domain. To understand this, let's consider the following example, given these constraints: \begin{cases} x + y = 8 \\ x - y = 1 \end{cases} and we can conclude that these constraints are satisfiable on domain ℝ, but not on domain ℤ.
There is one important special case for the LA on domain ℤ, which is called the 0-1 integer linear arithmetic (or 0-1 ILA). In this case, all integer variables can only be of two values: \(0\) or \(1\), in this sense, they correspond, perfectly, to boolean values (true or false).
The 0-1 Integer LA (as well as the 0-1 Integer Linear Programming we'll be discussing in the following) has many nice properties and many important applications, we'll discuss some in the following. But for now, let's start by considering one interesting problem, to let us appreciate 0-1 ILA's simplicity and power.
The problem is this: suppose we are given a list \(l\) of integers $$ [e_1, e_2, \ldots, e_n], $$ and we are required to write a program, to check whether there is at least one zero \(0\) in the list \(l\).
Of course, it's not to write a simple Python program to solve this problem. But for our purpose, let's consider how to solve this problem using 0-1 integer LA. For this, let's first declare a list \(X\) of auxiliary 0-1 integer variables $$ [x_1, x_2, \ldots, x_n], $$ which satisfy $$ x_i\in\left\{0, 1\right\}, \text{ for } 1 \le i\le n, $$ and also $$ \sum_{i=1}^{n} x_i = 1. \tag{1} $$
Informally speaking, there is just one \(1\) in the list \(X\). For the given input integer list \(l\) (which is being searched for \(0\)s): $$ [e_1, e_2, \ldots, e_n], $$ we require $$ \sum_{i=1}^{n} \left(x_i*e_i\right) = 0. \tag{2} $$
In previous sections, we've always been talking about the linear arithmetics, but many solvers, including Z3, also support the satisfiability solving on non-linear constraints.
Suppose we want to check the constraint $$ x * x = 2, $$ we can write (as we may expect):
x = Real('x')
res, model = check_cons([x * x == 2])
if res == sat:
print(model)
else:
print(res)
One important application of the non-linear arithmetic is to reason constraints on rational domain \(\mathbb{Q}\). We have studied linear arithmetic both on the real domain ℝ and the integer domain ℤ, Z3 has built-in supports for these two domains. However, the bad news is that Z3 does not support rational domain \(\mathbb{Q}\) directly. To mitigate this, we can use a very important property of rational numbers: suppose \(x \in \mathbb{Q}\) is a rational number, then we have $$ x = p/q \tag{3}, $$
for $$ q \neq 0, $$ where \(p, q \in \mathbb{Z}\). The formulae \((3)\) can be rewritten into $$ x*q = p \tag{4}. $$ Please notice that the equation \((4)\) is also non-linear.
Let's study one example to see how this strategy works in practice, consider our previous example once again, we can check the constraint $$ x*x = 2 \tag{5} $$ on rational domain \(\mathbb{Q}\), it's unsatisfiable.
In this section, we will study how to establish models and solve problems using the LA/LP theories, with the aid of the Z3 solver.
To be specific, we'll solve several very hard problems, by "hard", we mean that these problems are all NP-complete, that is, there are no known polynomial algorithms for these problems in general.
However, you will soon see that how easy (and how fun) it is to solve these problems with LA/LP solvers, such as Z3. And you'll acknowledge the power and simplicity of the solver-based problem-solving strategy, in general.
The NP-Complete problems that we'll be solving are (some of them have been discussed in our previous lectures):
Note that this is not a complete list of problems that an SMT-based solver can handle, after you have learned this technique, you are encouraged to try to solve other NP-Complete problems as well.
The subset problem is a well-known satisfiability problem: given a multiset (a multiset is like a normal set, expect for the elements can be duplicated) \(S\), we should decide a non-empty subset \(T\) of \(S\), such that $$ \sum T = 0, \text{ where } T \subseteq S. $$
For example, given this set $$ \left\{-7, -3, -2, 9000, 5, 8\right\}, $$ the answer is yes because this subset $$ \left\{-3, -2, 5\right\} $$ sums to zero.
This problem is NP-Complete, and for more background information of the subset problem, please refer to this article on the subset sum problem.
In practice,the subset sum problem can be solved in pseudo-polynomial time using dynamic programming.
In the assignment 3 (challenge problem), we've solved the
n-queen problem
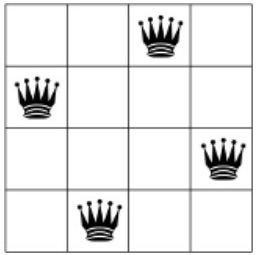
(4 Queens) by SAT. The problem is about placing \( N \) chess queens on an
\( N*N \) chessboard, so that no two queens threaten each other.
A solution requires that no two queens share the same row, column, diagonal
or anti-diagonal. The following figure shows a solution to the sample
n-queen puzzle where \( N = 4 \):
 The problem's target is try to find how many solutions exist, for
a \(N*N\) chess board.
The problem's target is try to find how many solutions exist, for
a \(N*N\) chess board.
The basic idea of SAT implementation is to construct the n-queen puzzle constraints by Bool values. Actually,we can solve n-queen problem by LA, which is much easier to understand and more efficient compare to SAT. The idea is same with the solution of subset sum problem. We use a two-dimensional 0-1 flag \(F\) to represent each cell of the chessboard, the \(F\) has value: $$ F[i][j] = \begin{cases} 0, & \text{if cell in $i$ row $j$ column is not placed a queen}; \\ 1, & \text{if cell in $i$ row $j$ column is placed a queen}; \\ \end{cases} $$ where \(0 \le i \lt N\) and \(0 \le j \lt N\). We can establish the constraints of the n-queen puzzle as follows:
Another method to solve the n-queen problem is to use the backtracking algorithm, but the complexity is exponential with respect to the chess board size \(N\).
The above LA implementation is not the unique algorithm to solve n-queen problem. In fact, the way we establish constraints to describe a problem often has a big impact on the efficiency of the algorithm.
Generally speaking, a linear programming problem (shorted as LP in the following) consists of two parts: the constraints \(C\) and the target function \(F\). And our goal is to get the minimal or the maximal values of \(F\) under the constraint \(C\). Both the constraints and the target function are of linear forms. In this part, we will study some LP problems, also with the aid of Z3.
For example, given the constraints \begin{cases} x &\lt 2 \\ y - x &\lt 1 \\ \end{cases} we want to calculate $$ \max\left(x + 2y\right). $$
To solve LP with Z3, we'll be using the Optimize module and, to be specific, the maximize() API. For more details about the module and the API, you can refer to the official documents.
For the above example, we can have the following Z3 code:
x, y = Ints("x y")
solver = Optimize()
cons = [x < 2, (y - x) < 1]
solver.add(cons)
solver.maximize(x + 2*y)
if solver.check() == sat:
print(solver.model())
Z3 will output some result like this:
[y = 1, x = 1]
The knapsack problem is a typical optimization problem,which has been studied for hundreds of years. The problem is: given a set of items, each item has a weight and a value, determine the number of items such that the total weight is less than a given limit and the total value is as large as possible. There are a number of sub-problems of the knapsack problem: 0-1 knapsack problem, complete knapsack problem, multiply knapsack problem, multidimensional knapsack problem and so on. Please refer to knapsack problem to get more information.
Let's discuss 0-1 knapsack problem first, which assumes that there is only one quantity per item. In the following, we use the following notations: \begin{align} W: &\text{ item's weight}\\ V: &\text{ item's value}\\ C: &\text{ the bag's capacity}\\ \end{align} and we use a flag \(F\) for each item with $$ F[i] = \begin{cases} 0, & \text{if item $i$ is not chosen}; \\ 1, & \text{if item $i$ is chosen}. \\ \end{cases} $$ To guarantee that the total weight can not exceed the bag capacity \(C\), we have $$ \sum_{i=0}^{N-1} \left(F[i]*W[i]\right) \le C, $$ where \(N\) is the total number of items. The goal of our optimization is to maximize the value of the chosen items $$ \max\left(\sum_{i=0}^{N-1} \left(F[i]*V[i]\right)\right). $$
Another sub-problem of knapsack problem is the complete knapsack problem, which assumes that the number of items of all kinds is unlimited, your can choose one kind of item any times. So we need to declare a variable for each kind of item \(F\) have chosen by amount \(A\): $$ F[i] = A, $$ where \(0 \le i \lt N\) and \(0 \le A\). So the constraint of total weight is $$ \sum_{i=0}^{N-1} (F[i]*W[i]) \le C, $$ where \(N\) is the total number of the kinds of items. The maximal value of the chosen items is $$ \max\left(\sum_{i=0}^{N-1} (F[i]*V[i])\right). $$
The knapsack problem can also be solved by dynamic programming.
In statistics, a linear regression is a linear approach to modelling the relationship between a scalar response and one or more explanatory variables (also known as dependent and independent variables).
In recent years, linear regression plays an important role in the field of artificial intelligence and machine learning. The linear regression algorithm is one of the fundamental supervised machine learning algorithms for its relative simplicity and well-known properties. Interested readers can refer to materials on deep learning, for instance, Andrew Ng gives a nice introduction to linear regression from a deep learning point of view (up to page 7).
However, as this is not a deep learning course, so we'll get access to the problem from the mathematical point of view. We start by studying one concrete example, given the following data (in deep learning's terminology, these are called the training data): \begin{align} X &= [1.0, 2.0, 3.0, 4.0]\\ Y &= [1.0, 3.0, 5.0, 7.0] \end{align} Our goal is to produce a linear function: $$ y = k*x + b, $$ such that it fits the above data as close as possible, where the variables \(k\) and \(b\) are unknown variables. By "as close as possible", we use a least squares method, that is, we want to minimize the following expression: $$ \min\left(\sum_{i=0}^{N-1} (Y[i] - (k*X[i]+b))^2\right), \tag{6} $$ where \(N\) is the length of \(X\) or \(Y\).
Now the next step is to solve the equation \((6)\) to calculate the values for the variables \(k\) and \(b\). We will use the Z3 to finish this task, as Z3 also supports some non-linear constraint solving.
The popular approach used extensively in deep learning is the gradient decedent algorithm, if you're interested in this algorithm, the above Andrew Ng's notes contains a nice introduction. In most situations, you don't need to re-invent the wheels, there are lots of efficient machine learning libraries in Python, say, the scikit-learn. You can use them directly to finish the task.
All problems in this section are optional!
In the lecture, we've discussed three algorithms for solving LA constraints: the Fourier-Motzkin variable elimination algorithm, the Simplex algorithm, and the branch-bound algorithm. In this part of the assignment, you will implement the former two of them.
Before we start implementing the algorithms, let's introduce some helpful data structures.
First we need a data structure to describe the inequalities, To simplify things here, we assume that all the constraints conform to the syntax for LA which is introduced in Part A section. It means that all the constraints only take \(=\) or \(\le\) or \(<\) as relation operator.
The data structure in the constraint.py Python file may suitable for describing a proposition in LA theory,but it's really not convenient to implement the LA algorithms by using them。Implementing a convenient data structure cost you a lot of time. Fortunately, some libraries provide us these facilities. To be specific, we'll be using the library pandas, which is a powerful and easy-to-use open source library. By using the DataFrame data structure in pandas to store the LA proposition, we will save a lot of engineering efforts.
The Fourier-Motzkin elimination method, also known as the FME method, is a mathematical algorithm for eliminating variables from a system of linear inequalities. It can operate on variables from real domains. The algorithm can be summarized as the following steps:
Assumes we want to solve the proposition \(P\) based on LA theory. The first step is find the constraints which contain \(=\) relation operator $$ \sum_{j=1}^{n}a_{ij} * x_j = b_i, $$ and rewrite them to $$ x_p = \frac{b_i}{a_{ip}} - \sum_{\substack{1 \leq j \leq n \\ j \neq p}} \frac{a_{ij}}{a_{ip}} * x_j. \tag{7} $$ Replace all the variable \(x_p\) in proposition \(P\) by the equation \((7)\). It can elimination the equation and all the variable \(x_p\) in proposition \(P\). Do this for all the equations in \(P\) and rewrite the proposition \(P\) to $$ \bigwedge\limits_{i=1}^m\sum_{j=1}^{n}a_{ij} * x_j \leq b_i. $$
In LA theory proposition \(P\), the variable \(x_p\) have no lower bound if all the coefficients of variable \(x_p\) are positive;the variable \(x_p\) have no upper bound if if all the coefficients of variable \(x_p\) are negative. We call a variable an unbounded variable if it has no upper bound or no lower bound,on the contrary, a bounded variable has both upper bound and lower bound. Unbounded variables can be simply removed from the proposition \(P\) together with all constraints that use them. Removing these constraints can make other variables unbounded. Thus, this simplification stage iterates until no unbounded variables remain.
If there is no unbounded variable in the proposition \(P\), we can choose one bounded variable to eliminate. The choice of variables is heuristic, we assume that the chosen variable is \(x_q\). We can get an upper bound of variable \(x_q\) by $$ x_q \leq \frac{b_i}{\lvert a_{iq} \rvert} - \sum_{\substack{1 \leq j \leq n \\ j \neq q}} \frac{a_{ij}}{\lvert a_{iq} \rvert} * x_j $$ if \(a_{ij} > 0\), and get one lower bound by $$ x_q \geq \sum_{\substack{1 \leq j \leq n \\ j \neq q}} \frac{a_{ij}}{\lvert a_{iq} \rvert} * x_j - \frac{b_i}{\lvert a_{iq} \rvert}, $$ if \(a_{ij} < 0\). Assume there are \(m\) positive and \(n\) negative occurrences of \(a_{ij}\) in proposition \(P\), we can set the upper bounds as $$ U_1(x),\dots, U_m(x), $$ and the lower bounds of proposition \(P\) as $$ L_1(x), \dots, L_n(x). $$ Let's continue to assume that there are \(k\) constraints do not contain the variable \(x_q\): $$ D_1(x),\dots,D_k(x). $$ We need all the lower bounds smaller than the upper bounds of variable \(x_q\) if we want to eliminate it. So we need compare them one by one and get the proposition without variable \(x_q\): $$ \left( \bigwedge\limits_{j=1}^m \bigwedge\limits_{i=1}^n(L_i(x) - U_j(x) \leq 0) \right) \bigwedge \left(\bigwedge\limits_{r=1}^k D_r(x) \right). $$ After eliminate the bounded variable \(x_q\), if there only have one variable left in proposition \(P\), go to step 4. Or else, go back to step 2.
Running an elimination step over n inequalities can result in at most \((m^2)/4\) inequalities in the output, if the proposition \(P\) has \(m\) constraints and \(n\) variables. Thus running the successive steps can result in at most \(m^{2^n}/4^n\) complexity.
Simplex algorithm is originally developed to solve the linear programming (LP) problems by George B. Dantzig in 1947, and SMT for LA is a sub-problem of LP in which there is no the optimization goal. The key idea of Simplex algorithm can be divided into the following steps:
The pivot operation performs a key role in this step. For example, if we want pivot \(s_0\) and \(x_0\) in the tableau \((11)\). The first step of the pivot operation is to solve the row of \(s_1\) for \(x\): $$ s_0 = x_0 + x_1 \Leftrightarrow x_0 = s_0 - x_1; $$ This equality is now used to replace \(x\) in the other two rows: $$ s_1 = 2(s_0 - x_1) - x_1 \Leftrightarrow s_1 = 2s_0 - 3x_1; $$ $$ s_2 = -(s_0 - x_1) + 2x_1 \Leftrightarrow s_2 = -s_0 + 3x_1. $$ Tableau \((11)\) is rewritten as $$ \begin{array} {r|r} & s_0 & x_1 \\ \hline x_0 & 1.0 & -1.0 \\ \hline s_1 & 2.0 & -3.0 \\ \hline s_2 & -1.0 & 3.0 \\ \end{array} $$
simplex(){
tab = constructTableau();
while(True){
for(each additional var si){
if(si violates its constraint){
if(there is a suitable xj){
pivot(si, xj);
update additional var
}
else return UNSAT;
}
}
if (each additional var satisfies its constraint)
return SAT;
}
}
Don't forget to test your simplex algorithm solution, by using unit test
case in the file.
Happy hacking!